How do we measure MEG?
Conventional MEG scanner
A typical MEG device consists of 100-300 highly sensitive sensors arranged around the subject’s head. Conventional MEG uses extremely sensitive magnetic field sensors, so-called superconducting quantum interference devices or SQUIDs. As the name suggests SQUIDs require superconductivity to work. Superconductivity is a quantum physical state where the material becomes a perfect electric conductor and expels magnetic fields. To date, superconductivity can only be achieved at cryogenic temperatures (and/or extreme pressures). Conventional SQUIDs must be cooled to less than ~9 K (~-265 °C). This is usually achieved with liquid helium (~4 K; ~-269 °C) and requires substantial thermal insulation between the cold sensors and the room temperature environment. The thermal insulation in a MEG device is achieved by a combination of superinsulating foil and ~2 centimeters of vacuum. The MEG sensors are housed inside a double walled flask, where the volume between the two walls is hermetically sealed and vacuum pumped (similar to a thermos bottle).
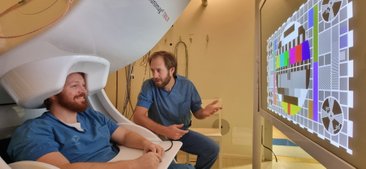
Figure 1: Photo of a recording with a conventional MEG scanner at NatMEG
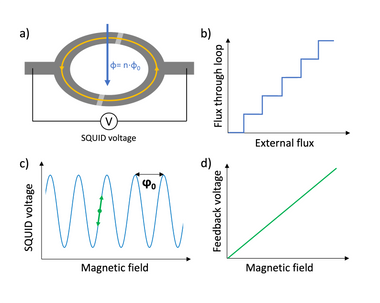
A SQUID consists of a superconducting loop with two weakly or non-superconducting links (Figure 2-a). Superconducting rings have the interesting property that they only permit flux in discreet steps through them – in other words the flux through a superconducting loop is quantized. If the externally applied field is larger or smaller than an integer multiple of the flux quantum, a current is induced that brings the total flux through the loop to the closest integer (Figure 2-b). Since superconductors exhibit zero resistance, these currents could normally not be measured. Here is where the weak links come in. Unlike in the superconductor, the current through a weak link generates a voltage that can be measured. Unfortunately, the induced voltage has a periodic relation with the magnetic field with the period equal to the flux quantum – which would severely limit the range in which the sensor can measure (Figure 2-c). To linearize the signal, a negative feedback loop is created with a small coil which counters any change in in the external magnetic field by generating an opposing field that keeps the SQUID voltage at a fixed point (called the working point; indicated by green dot in Figure 2-c). The current going to the feedback coil has a linear relation with the measured magnetic field and serves as the sensor output signal (Figure 2-d).
SQUIDs are usually very small, only some tens to hundreds of micro(10-6)meter, which is suboptimal for magnetic field sensitivity. To increase magnetic field sensitivity, SQUIDs can be connected to a flux transformer consisting of a larger (pick-up) coil connected to smaller (coupling) coil. A flux transformer can be imagined as a funnel, that picks up the magnetic field over a large area and concentrates it onto the small area of the SQUID loop. Flux transformers are typically also superconducting, often even integrated into the same chip as the SQUID. Together the flux transformer and SQUID form the MEG sensor.
Figure 2: a) Schematic of a SQUID consisting of a superconducting ring (dark grey) with two weak links (light grey). Externally applied magentic field and induced current are indicated by blue and yellow arrows respectively. b) Flux quantization. c) SQUID voltage as a function of externally magnetic field. Working point of negative feedback scheme is indicated in green. d) SQUID output signal.
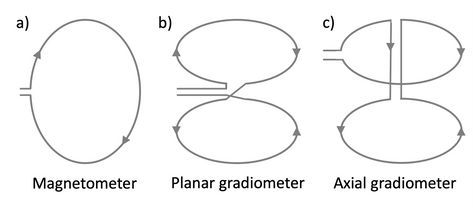
Pick-up coils (the large input coil of a flux transformer) come in different forms and shapes that affect how the combined sensor measures the magnetic field. They can be roughly divided into two categories. Simple loops create magnetometers - sensors whose output is proportional to the magnetic field through the loop. Double loops with opposing windings, such as a figure-8 coil, create gradiometers - sensors whose output is proportional to the difference between the magnetic fields through the different loops. In the figure-8 coil example, that would be the difference between top and bottom loop which would effectively result in measuring the vertical gradient of the magnetic field that is perpendicular to the plane (i.e., that points out of the page or screen). Higher order gradiometers can be achieved with more complex pick-up loop configurations.
Figure 3: Example of pickup loops forming a magnetometer (a) and planar gradiometer (b)
The advantage of gradiometers lies in the fact that, while they are less sensitive than a magnetometer of the same size, they suppress external interferences. A faraway source, like a car driving by, will create an equal magnetic field in both loops and get cancelled out (assuming the two loops are the same and opposite wound), while a close source, such as neuronal activity will create different magnetic fields in the two loops. Typical MEG scanners use magnetometers and/or first-order gradiometers.
Magnetically shielded room
MEG scanners operate inside a magnetically shielded room, or MSR for short, that deflects most of the external magnetic interference from the environment that would otherwise mask the weak fields from the brain. For perspective, typical MEG fields are on the order of several tens to hundreds of femto(10-15)-tesla, roughly a hundred million to a billion times smaller than the earth’s magnetic field that is approximately 50 micro(10-6)-tesla. MSRs are constructed from multiple layers of high permeability metal, e.g., mu-metal, a ferromagnetic nickel-iron alloy, that deflect low frequency magnetic fields and high conductivity metal, e.g., copper, that shields high frequency magnetic fields. Some MSRs have additional active compensation where external fields are cancelled by generating opposing fields with coils, e.g., in the MSR walls.
Figure 4: Schematic of a magnetically shielded room housing a MEG scanner illustrating how the magnetic shielding (grey squares) diverts external magnetic fields (blue arrow).